Real numbers are probably the most oxymoronically named numbers in all of mathematics. There is almost nothing “real” about them. In some sense, even the imaginary number, $i$, is more real. Before we get into the “unrealness” of the reals, first let’s review some basic arithmetic.

In the beginning, we have the natural numbers, $\mathbb{N}$, which are the positive, whole numbers, like $1$, $2$, $3$. Then by adding zero and negative whole numbers, we have the integers, $\mathbb{Z}$. If we start dividing whole numbers, we get all the fractions, or rational numbers, $\mathbb{Q}$. Going further, if we look at all the numbers that are possible solutions to polynomial equations with rational coefficients, we get what are called algebraic numbers. These numbers are named as such because they are the primary subjects studied under algebra. Included in them are many irrational numbers like $\sqrt{2}$. Then we have the real numbers, $\mathbb{R}$, which are, informally, all the numbers on the number line. The set of real numbers includes all the previous sets of numbers, of course. Here’s a simple diagram illustrating the types of numbers we just outlined:

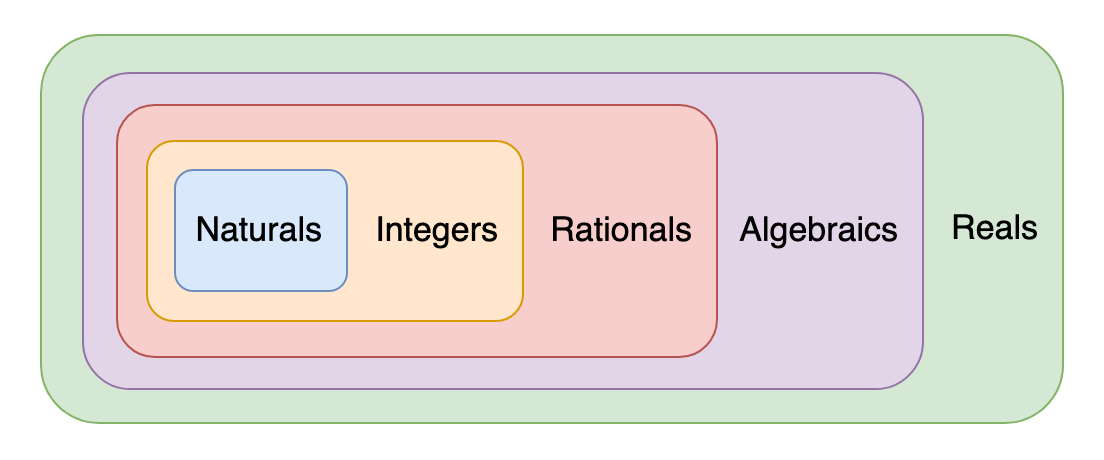
The first thing to point out is that this diagram is absolutely not-to-scale. If it were, everything inside the purple box would be invisible - not even as a single purple pixel within the large green box. This is because there is only a countably infinite number of algebraic numbers, while the size of the reals is uncountably infinite. Yes, there are different levels of infinities, and roughly speaking, the difference between countable infinity and uncountable infinity is whether you can systematically and reliably list out all the numbers in the set, given an infinite amount of time.

This brings us to the first major unrealness of the reals: almost all real numbers cannot be defined. And I mean this with the mathematical definition of “almost all” (i.e. all but a negligible amount¹) and the broadest sense of the word “defined”. To specify or refer to a number, we typically assign a particular or a set of symbols to it. $1$ specifies/defines the number one, trivially. $\frac{1}{3}$ defines the number $0.33333…$ - even though the full decimal representation of the number contains an infinite number of digits, we have a convenient fractional shorthand for it. Similarly for algebraic numbers, we can refer to them unambiguously by using the polynomials for which they are the solutions for. We may have to additionally specify which exact solution (or root) we are referring to, as many polynomials have multiple roots, but it is easily doable for all the algebraics.

For non-algebraic reals (also known as transcendental numbers) - the numbers that lie outside the purple box, strictly in the green section above - we aren’t so lucky. Sure, there are a few of them that are within our grasp, $\pi$ and $e$ for example, but almost all of them are beyond our ability to even conceptually define. We have ascribed the special symbol $\pi$ to the particular transcendental number that is the ratio of a circle’s circumference to its diameter, defining its exact value symbolically. Furthermore, we can compute it to an arbitrary precision, because of its special properties and relationships with other well-known entities (e.g. equations of circles). But this is an extremely rare exception. Almost all other transcendental numbers (which make up almost all of the reals) contain an infinite number of digits without any pattern, and have no special properties nor relationships with anything else we know. To define them by associating symbols to them (including using natural language descriptions, such as “the second smallest real number less than 1”) would be futile, as it would require an uncountably infinite number of symbols. And even if we could represent them symbolically, it would be pointless anyway as we have absolutely no way to calculate them, not even approximately. In theoretical computer science, they are called uncomputable numbers: their values cannot be computed to arbitrarily close approximations by any Turing machine.

(The fact that almost all real numbers are uncomputable, undefinable, and unrepresentable has led to some mathematicians, notably the constructivists, contemplating completely removing all the uncomputable reals from mathematics, since we can’t really work with them directly anyway. But doing so has some significant implications and results in a very different form of mathematics, so most people have chosen not to do this.)

We’ve already seen that there is an uncountably infinite number of real numbers, which is far, far, greater than the number of algebraic numbers. But it gets crazier. There is actually an uncountably infinite number of real numbers between any two unequal real numbers, no matter how close they are. Since there is only a countably infinite amount of numbers that we can define and compute (after all, there are only countably many Turing machines), all the numbers that we can ever know can fit, in terms of size of the set, within the gap between two arbitrarily close real numbers. And it’s not a tight fit either, the fit is in the same manner that algebraic numbers fit inside the real numbers - basically taking up 0 space. It isn’t an exaggeration at all to say that everything that exists in the entire known universe is nothing compared to what resides between two real numbers.

Speaking of the universe, this brings me to the last unrealness of the reals that I’ll talk about here, and it has to do with reality itself. If any transcendental real numbers actually existed in some physical form in the universe (yes, even just one), then the fundamental nature of reality would be very different from our current conception. First, it would mean that the universe is in some sense infinite, since it would necessarily contain an infinite amount of information just from having a single transcendental number in it². Second, it would mean that our universe is fundamentally continuous, not discrete. There would be no smallest increment of space (and possibly time too); lengths, volumes, velocities can vary arbitrarily, at least in theory. If such a physically real transcendental number can be somehow utilized for computation, it could potentially allow for forms of hypercomputation - computation whose power exceeds that of Turing machines. The halting problem could be solvable. Gödel’s incompleteness theorems could be invalidated, since they are based on the power of systems equivalent to Turing machines. And front-end web development might actually no longer be a mess.

If all that sounds insane, it’s because it definitely is. Almost all real numbers are absolutely, totally unreal! And even though these wild, nonsensical ideas may seem pointless, I find that learning about them is a truly humbling experience. It’s one thing to realize the insignificance of our abilities within the vast cosmos. But it’s another level of awe to realize that even within the domain of our own creation - pure, abstract mathematics - we are also inconsequentially limited.